3.4 스트링 편집 거리 문제
3.4.1.개념과 원리
편집 거리 ( edit distance ) : 두 문자열 사이의 근접성 또는 유사성을 판단하는 척도로, 철자 검사기에서 잘못된 철자를 만나면 해달 철자와 가장 근접한 다른 단어를 찾아주는데 활용
- 두 문자열 사이의 근접성 또는 유사성을 판단하는 척도
- 두 문자열 사이에 편집이 필요할수록 비용이 커지는 구조
X=x1x2…xn Y=y1y2…ym
문자열 X를 Y로 변환하는 데 필요한 전체 편집 연산에 대한 최소 비용
- 특정 위치에 새 문자를 삽입하는 연산 → 삽입 비용 δi
- 특정 위치의 문자를 삭제하는 연산 → 삭제 비용 δd
- 특정 위치의 문자를 다른 문자로 변경하는 연산 → 변경 비용 δc

스트링 편집 거리에서의 최적성의 원리
X와 Y사이의 편집 거리는 이들의 부분 문자열 사이의 편집 거리를 포함
X의 마지막 글자가 Y의 마지막 글자와 같거나 같게 변경된 경우
x1x2…xn-1과 y1y2…ym-1의 최소 편집 비용 + 마지막 글자의 변경 비용 δC(일치한 경우에는 비용 0)
X의 마지막 글자가 삭제된 경우
x1x2…xn-1과 y1y2…ym의 최소 편집 비용 + X의 마지막 글자의 삭제 비용 δD
Y의 마지막 글자가 삽입된 경우
x1x2…xn과 y1y2…ym-1의 최소 편집 비용 + Y의 마지막 글자의 삽입 비용 δI
스트링 편집 거리 문제의 점화식
Xi=x1x2…xi와 Yj=y1y2…yj 사이의 편집 거리

3.4.2. 알고리즘
ED(n,X[],m,Y[],ins,del,chg)
입력 :문자 배열 X[1..n],Y[1..m]
삽입 비용 ins,삭제 비용 del,변경 비용 chg
출력 :E[n][m]:편집 거리
{
int E[n+1][m+1],i,j;
E[0][0]=0;
for(i=1;i<n+1;i++) //첫 열의 초기화
E[i][0]=E[i-1][0]+del;
for(j=1;j<m+1;j++) //첫 행의 초기화
E[0][j]=E[0][j-1]+ins;
for(i=1;i<n+1;i++) for(j=1;j<m+1;j++)
{
c=(X[i]==Y[j])?0:chg;
E[i][j]=min(E[i-1][j]+del,E[i][j-1]+ins,E[i-1][j-1]+c); // 점화식
}
returnE[n][m];
}

3.4.3 성능 분석

각 열의 삭제비용으로 초기화 O(n) , 각행의 삽입비용으로 초기화 O(m) , n. m dl 첩되어 있는구간 O(nm)
3.4.4 특징
P ( i , j ) ← E(i,j)로 선택되는 최솟값이 어떤 연산으로 결정되는 지를 표시
⇒ 적용된 편집 연산을 구할 수 있음
3.5 모든 정점 간의 최단 경로
3.5.1. 개념과 원리
두 정점 간의 최단 경로 ( shortestpath )
가중 방향 그래프에서 두 정점을 연결하는 경로 중에서 간선의 가중치의 합이 가장 작은 경로
유형
하나의 특정 정점에서 다른 모든 정점으로의 최단 경로
→ 데이크스트라Dijkstra 알고리즘 (욕심쟁이 방법)
모든 정점에서 다른 모든 정점으로의 최단 경로
→ 플로이드 (Floyd) 알고리즘
모든 정점 간의 최단 경로
가정 -> 가중치의 합이 음수인 사이클은 존재하지 않음
플로이드 알고리즘
- 동적 프로그래밍 방법 적용
- 간선의 인접 행렬 표현을 활용하여 경유할 수 있는 정점의 점위가 1인 경로부터 시작해서 |V| 까지의 단계적으로 점위를 늘려가면서 모든 정점 간의 최단 경로를 구하는 알고리즘
→ 가중치의 합이 음수인 사이클이 없는 경우에 적용 가능

플로이드 알고리즘 점화식
D ( i, j, k ): 정점 1부터 k까지의 정점만 경유할 수 있는 정점 i에서 j까지의 최단 경로

3.5.2. 알고리즘
Floyd(G)
입력 : G = ( V, E )
출력: D[][]:모든 정점에서 모든 정점으로의 최단 경로의 길이
{
D[][]←입력 간선의 인접 행렬로 초기화
for(k=1부터 |V|까지)
for(i=1부터 |V|까지)//시작 정점
for(j=1부터 |V|까지)//끝 정점
if(D[i][j]>D[i][k]+D[k][j])
D[i][j]=D[i][k]+D[k][j];
returnD[][];
}
3.5.3. 성능 분석
Floyd(G)
{
D[][]←입력 간선의 인접 행렬로 초기화 >>> O( |V|^2 )
for(k=1부터 |V|까지) --------------
for(i=1부터 |V|까지) --------------
for(j=1부터 |V|까지) -------------- >>>> O ( |V|^3 )
if(D[i][j]>D[i][k]+D[k][j]) --------------
D[i][j]=D[i][k]+D[k][j]; --------------
returnD[][];
}
알고리즘의 시간 복잡도는 O ( |V|^3 ) 이다.
3.5.4 특징
최단 경로 자체를 구할 수 있음

3.6 저울 문제
3.6.1 개념과 원리
저울 문제
양팔 저울,n개의 추,각 추의 무게 wi (1≤i≤n)
무게 M인 물체를 양팔 저울로 달 수 있는 지 확인하는 문제
추의 무게 Wi와 물체의 무게 M은 모두 정수라고 가정
저울 문제에서의 최적성의 원리
선택된 k개의 추(s1,s2,…,sk) → M = Ws1 + Ws2 + ........... + Wsk
선택된 추에 n번 추가 포함되지 않는다면
1~(n-1)번까지의 추를 이용하여 무게 M인 물체를 달 수 있는 지의 문제
선택된 추에 n번 추가 포함된다면 (sk=n이라고 가정)
n번 추를 제외시키면 → Ws1 + Ws2 + ........... + Wsk-1 = M - Wsk
1~(n-1)번까지의 추를 이용하여 무게 인 물체를 달 수 있는 지를 확인하는 문제

3.6.2 알고리즘

3.6.3 성능분석

3.6.4 특징
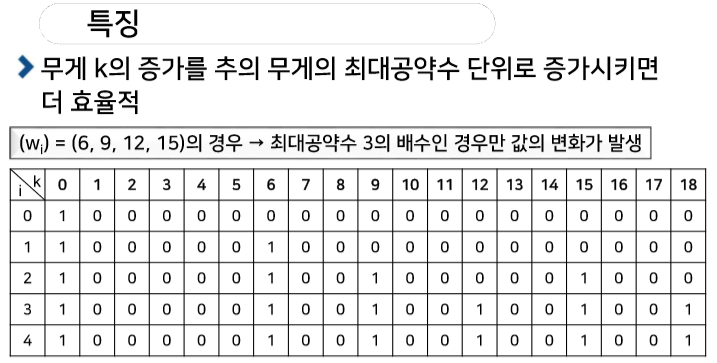

물체의 무게가 2n보다 크면 모든 경우를 따져 보는 직관적인 방법보다 비효율적
- 직관적 알고리즘 → n개의 추로 조합 가능한 모든 경우의 수 → O(2^n)
- M>2^n이면 nM>n2^n>2^n이므로 O(nM)인 알고리즘이 직관적인 알고리즘보다 비효율적
M과 wi가 정수가 아니면 동적 프로그래밍 방법 적용 불가
- 추의 무게와 물체의 무게에 제한 없는 저울 문제 → 되추적 알고리즘
5강 제3장 동적 프로그래밍 알고리즘
5강 제3장 동적 프로그래밍 알고리즘
학습목표 1. 동적 프로그래밍 방법의 개념과 적용 단계를 이해할 수 있다. 2. 피보나치 수열 문제를 통해 분할정복 방법과의 차이를 이해할 수 있다. 3. 연쇄 행렬 곱셈 문제의 개념, 동장, 그리고 특징을 이해할..
3catpapa.tistory.com
7강 제 4장 욕심쟁이 알고리즘
7강 제 4장 욕심쟁이 알고리즘
학습목표 1. 욕심쟁이 방법의 개념과 원리를 이해할 수 있다. 2. 동전 거스름돈 문제와 배낭 문제의 개념, 동작, 그리고 특징을 이해할 수 있다. 3. 최소 신장 트리와 최단 경로를 구하는 방법의 개념, 동작, 그리..
3catpapa.tistory.com
'방송통신대학 > 알고리즘' 카테고리의 다른 글
| 8강 제 4장 욕심쟁이 알고리즘 (0) | 2020.04.30 |
|---|---|
| 7강 제 4장 욕심쟁이 알고리즘 (0) | 2020.04.29 |
| 5강 제3장 동적 프로그래밍 알고리즘 (0) | 2020.04.28 |
| 4강 제2장 분할정복 알고리즘 2 (1) | 2020.04.27 |
| 3강 제 2 장 분할정복 알고리즘 (0) | 2020.04.26 |