학습목표
1. 동적 프로그래밍 방법의 개념과 적용 단계를 이해할 수 있다.
2. 피보나치 수열 문제를 통해 분할정복 방법과의 차이를 이해할 수 있다.
3. 연쇄 행렬 곱셈 문제의 개념, 동장, 그리고 특징을 이해할 수 있다.
4. 스트링 편집 거리 문제의 개념, 동작, 그리고 특징을 이해할 수 있다.
5. 모든 정점 간의 최단 경로를 찾는 문제의 개념, 동작, 그리고 특징을 이해할 수 있다.
6. 저울 문제의 개념, 동작, 그리고 특징을 이해할 수 있다.
주요용어
#최적화문제 #상향식접근 #최적성의 원리 #점화관계식 # 테이블 #피보나치수열 #연쇄행렬곱셈 #스트링편집거리 #최단경로 # 플로이드알고리즘 #저울문제
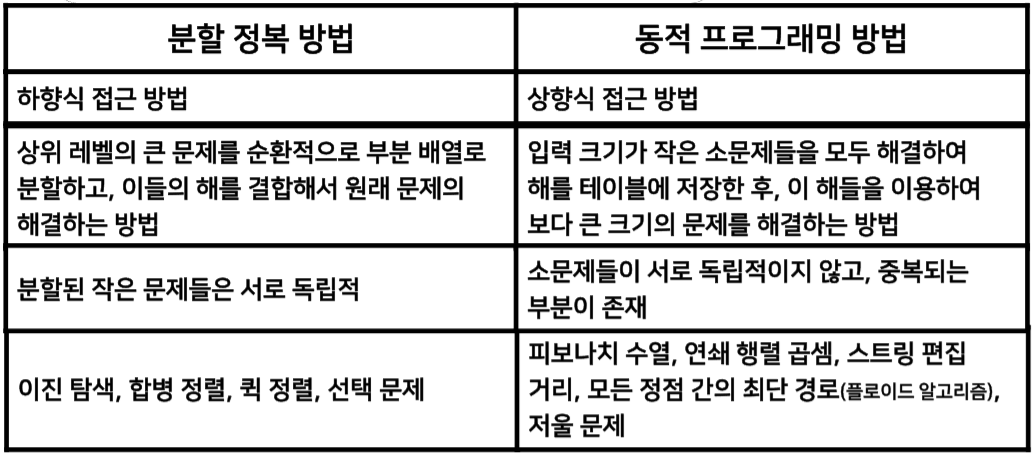
3.1. 동적 프로그래밍 방법의 원리
-동적 프로그래밍 ( dynamic programming ) 방법은 문제의 크기가 작은 소문제에 대한 해를 저장해 놓고 이를 크기가 보다 큰문제의 해를 점진적으로 만들어가는 상향식 접근 방법이다.
-최솟값 또는 최댓값을 구하는 최적화 문제에 주로 사용
-최적성의 원리
> 주어진 문제에 대한 최적해가 소문제에 대한 최적해로 구성된다는 원리
-동적 프로그래밍의 적용 단계
1. 주어진 문제에 대해서 최적해를 제공하는 점화식 도출
2. 가장 작은 소문제부터 점화식의 해를 구한 뒤 이를 테이블에 저장
3. 테이블에 저장되어 있는 ㅁ소문제의 해를 이용하여 점차적으로 큰 상위 문제의 해를 구함
3.2 피보나치 수열 문제
3.2.1. 개념과 원리

피보나치 수열은 정의 자체가 최적성의 원리가 성립되는 점화식이므로 바로 동적 프로그래밍 방법을 적용할 수 있다.
2이상이 n에 대해 f(n)은 그 소문제의 해인 f(n-1) 과 f(n-2)의 합으로 구성되므로, f(0) 과 f(1)을 먼저 테이블에 저장한 후 n 을 2부터 1씩 증가시키며 해를 구한 뒤 테이블에 저장한다.
3.2.2 알고리즘
Fibo(n)
입력 : n: 구하려는 피보나치 수열의순번
출력 : f[n] : 피보나치 수열 f(n)
{
f[0] = 0; f[1] = 1; // f(0)과 f(1)을 테이블에 저장
for ( i = 2 ; i < = n; i++) // i 를 2부터 1씩 증가시키며
f[i] = f [ i - 1 ] + f [ i - 2 ]; // f(i)의 해를 테이블에 저장된 f ( i - 1 )과 f ( i - 2 의
// 합으로 계산하여 다시 테이블에 저장
return f[n];
}
3.2.3 성능 분석
위 알고리즘의 for 루프는 구하려는 피보나치 수열의 순번 n 만큼 반복하므로 시간 복잡도는 O(n) 이다.
3.3 연쇄 행렬 곱셈 문제
3.3.1 개념과 원리
n 개의 행렬을 곱할 때 최소의 기본 곱셈 횟수를 가진 행렬의 곱셈 순서를 구하는 문제
i x j , j x k 행렬을 곱하는 데에는 i x j x k 번 만큼의 기본 곱셈이 필요하고 결과는 i x k 행렬을 얻는다.

n개의 행렬(M1,M2,…,Mn)을 연쇄적으로 곱하는 경우
결합법칙 성립
M1∙M2∙M3 → ((M1∙M2)∙M3) = (M1∙(M2∙M3))
여러 가지 다른 곱셈 순서가 존재 → 곱셈의 횟수가 달라짐
연쇄 행렬 곱셈 문제?
n개의 행렬을 연쇄적으로 곱할 때 최적의 곱셈 순서를 구하는 문제
⇒ 최소의 기본 곱셈 횟수를 가진 행렬의 곱셈 순서를 구하는 문제

연쇄 행렬 곱셈 문제에서의 최적성의 원리
n개의 행렬을 곱하는 최적의 순서는 n개 행렬의 어떤 부분집합을 곱하는 최적의 순서를 포함
7 개 행렬을 곱하는 최적의 순서 >>
(M1M2)((((M3M4)M5)M6)M7) >>
M 3,M4,M5를 곱하는 최적의 순서 ((M3M4)M5) >>
부분 문제들의 최적해로 n개 행렬을 곱하는 최적의 순서를 구할 수 있음 >>
최적성의 원리가 성립 >> 동적 프로그래밍 방법으로 해결 가능

3.3.2 알고리즘
MinMatMult (n,d[])
입력: 행렬의 개수 n,
d[0..n](i번째 행렬의 크기 d[i-1]´d[i])
출력: C[1][n]:n개의 행렬을 곱하는 데 필요한 곱셈 횟수의 최소값
P[1..n][1..n]:최적의 곱셈 순서를 구할 수 있는 배열
{
int i,j,k,s;
int C[n+1][n+1];
for(i=1;i<=n;i++)C[i][i]=0;
for(s=1;s<=n-1;s++)
for(i=1;i<=n-s;i++)
{
j=i+s;
C[i][j]=mini≤k≤j-1(C[i][k]+C[k+1][j]+d[i-1]d[k]d[j]);
P[i][j]=최소값이 되는 k의 값;
}
returnC[1][n];
}
3.3.3 성능 분석

알고리즘의 시간 복잡도는 O(n^3) 이다.
4강 제2장 분할정복 알고리즘 2
4강 제2장 분할정복 알고리즘 2
2.3 합병 정렬 2.3.1 개념과 원리 합병 정렬 ( merge sort ) 전형적인 분할정복 방법에 해당 배열을 동일한 크기의 두 개의 부분배열로 분할하고, 각각의 부분배열을 순환적으로 정렬한 후, 정렬된 두 부분배열을..
3catpapa.tistory.com
6강 제 3장 동적 프로그래밍 알고리즘
6강 제 3장 동적 프로그래밍 알고리즘
3.4 스트링 편집 거리 문제 3.4.1.개념과 원리 편집 거리 ( edit distance ) : 두 문자열 사이의 근접성 또는 유사성을 판단하는 척도로, 철자 검사기에서 잘못된 철자를 만나면 해달 철자와 가장 근접한 다른 단..
3catpapa.tistory.com
'방송통신대학 > 알고리즘' 카테고리의 다른 글
| 7강 제 4장 욕심쟁이 알고리즘 (0) | 2020.04.29 |
|---|---|
| 6강 제 3장 동적 프로그래밍 알고리즘 (0) | 2020.04.29 |
| 4강 제2장 분할정복 알고리즘 2 (1) | 2020.04.27 |
| 3강 제 2 장 분할정복 알고리즘 (0) | 2020.04.26 |
| 2강 제 1강 알고리즘 1.3 알고리즘 설계 (0) | 2020.04.25 |