이산 수학 과제 (풀이설명)

 

1) 문제

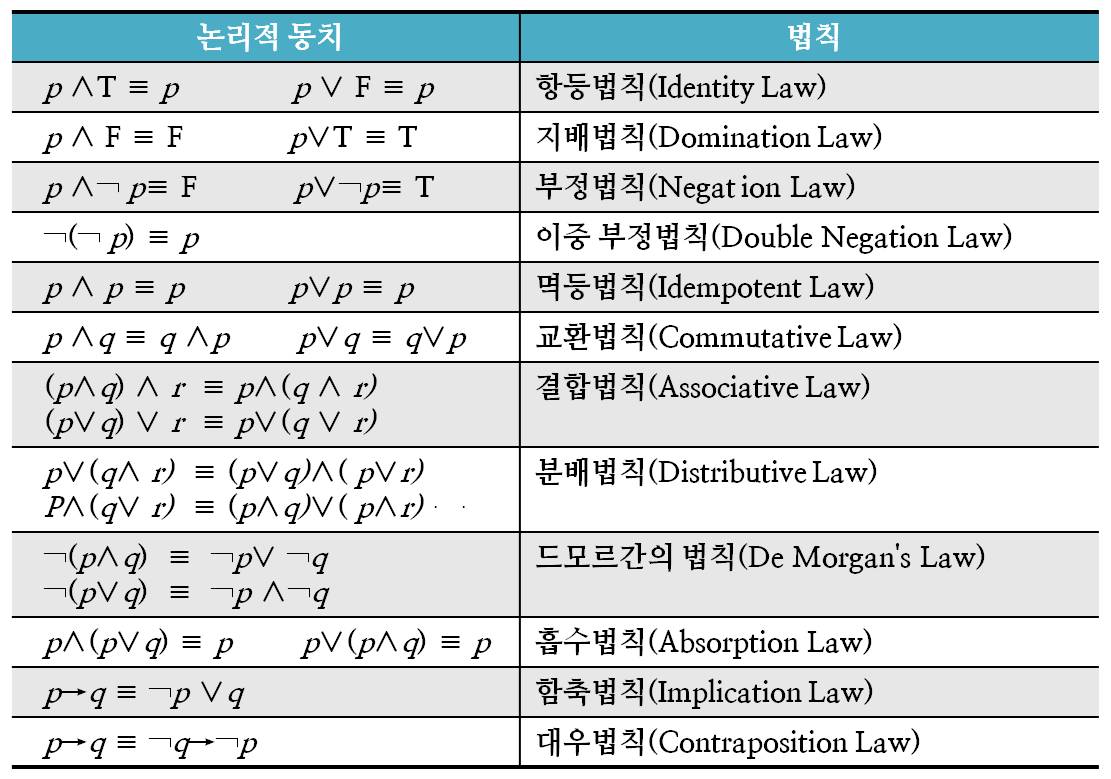
교제 제 2장 논리 표 2-8 

 

드모르간 법칙

분배 법칙

부정법칙

 

차례로 적용

 

 

 

 

 

 

 

2)   3.2 직접 증명법 (연역법)

명제를 변형하지 않고 증명하기 때문에 직접증명법이라고 한다. 주로, 공리와 정의, 그리고 이미 증명된 정리를 논리적으로 직접 연결해 증명하는 형식을 따른다.

 

예제 3.1 두 짝수의 합은 항상 짝수임을 증명하시오.

 

풀이 ) 두 짝수를 각각 x, y 라고 하면, 각각 x = 2a , y = 2b (a, b는 정수 ) 형태로 나타낼 수 있다.

x+y = 2a + 2b = 2 (a +b ) 이므로 두 짝수의 합은 항상 짝수이다.

 

-- 참고, 짝수 : 2로 나누었을때 나머지가 0 인수, 홀수 : 2로 나누었을때 나머지가 1인수 ( = 2a + 1)

 

 

3) 집합의 대수법칙

집합 A, B 가 유한집합이면 다음이 성립한다.

| A∪B | = |A| + |B| - |A ∩ B|

 

A∪B = = A ∪ ( B – A) 이고, A 와 B – A 는 서로소이므로
(1)    | A ∪ B | = |A| + |B-A|

 

B = ( B – A) ∪ ( A∩B ) 이고, B-A 와 A∩B는 서로소이므로
    | B | = | B-A | + | A∩B |
(2)    | B – A | = | B | - | A∩B |   

 

(2)번 식을 (1)번 식에 대입
| A ∪ B | = |A| + | B | - | A∩B |

 

 

 

4) 5.3 행렬의 종류 

정방행렬 (square matrix) (행 과 열 수가 같음 )

행의 수와 열의 수가 같은 n x n 행렬을 n 차 정방행렬이라고 하며,

n 을 정방행렬의 차수(order)라 한다. 

정방행렬의 각 원소를 대각 원소(diagocla entry) 라 하며,

대각 원소를 포함하는 대각선을 주대각선(main diagonal )이라 한다.

 

n 차 정방행렬은 다음과 같은 형태를 가진다. 

 

 

 

 

대칭행렬(symmetric matrix)

n 차 정방행렬에서 a12 = a21 인 행렬의 대칭행렬이라 한다.

다음과 같은 형태를 가지고 있다.

(A+A^T)T = A^T+(A^T)^T = A+A^T

교대행렬(skew matrix)  ( = 반대칭 행렬)

행렬 A=(aij )에서 aij = -aji 일 때 A는 교대행렬이고 대각원소 aij는 모두 0이다. 임의의 행렬은 대칭행렬과 교대행렬의 합으로 표시 할 수 있고 또 오직 하나로 정해진다. 다음 행렬 A는 교대행렬의 한 예이다.

=  ( A - A^T)^T  =  A^T -  A  = - ( A - A^T )

 

5) 제 6장 관계

동치류 (equivalence class )

집합 A에 대한 관계 R이 동치관계일 때,

A의 각 원소 a에 대하여 a의 동치류는 a와 R의 관계를 가지는 A의 원소들의 집합이며, [a]로 표기한다. 기호로 나타내면

[ a ] = { x ∈ A | aRx } 이다.

 

예제 ) 집합 A = {0, 1, 2 } 에 대한 관계 R이 다음과 같을 떄,

R이 동치관계임을 보이고 서로 다른 동치류를 모두 찾으시오.

 

R = { (0, 0), (1, 1), (1, 2), (2, 1), (2, 2) }

 

풀이 ) 

[ 0 ] = { 0 } , [ 1 ] = { 1, 2 },  [ 2 ] = { 1, 2 } 이므로, 서로 다른 동치류는 { 0 }, { 1, 2 } 이다.