주요용어
그래프 탐색 : 그래프 내 특정 정점을 찾는 연산, 트리와 다르게 루트노드가 없으므로 특정 정점에서 시작함(트리에서 노드로 부르는 것을 그래프에서 정점이라 함)
그래프 순회 : 특정 정점에서 시작하여 그래프의 모든 정점을 빠짐없이 그리고 중복 없이 방문하는 것
깊이 우선 탐색 : 그래프 순회 알고리즘의 하나로 특정 점정에서 시작하여 자손을 먼저 방문 한 후 (더 이상 방문 할 자손이 없으면) 전 단계 형제를 방문함
너비 우선 탐색 : 특정 정점에서 시작하여 모든 형제를 방문한 후 자손을 방문함
최소 비용 신장 트리 : 그래프의 모든 정점을 포함하는 사이클이 없는 부분 그래프 즉, 트리를 신장트리라 하며, 가중 그래프에서 비용이 최소인 신장 트리를 최소 비용 신장 트리라 함
01. 그래프의 탐색
그래프 탐색의 정의
- 그래프에서 특정 정점을 찾는 기본 연산
- 그래프 G = ( V, E)와 V(G)에 있는 정점이 v가 주어졌을 때, 정점 v 에 도달할 때까지 G의 정점을 방문하는 연산
-> 만일 없다면 그래프의 모든 정점을 방문한 후 종료함
- 그래프 순회에는 깊이 우선 탐색(DepthFirstSearch;DFS) 과 너비 우선 탐색(BreadthFirstSearch;BFS) 두 가지 방법이 있음
- 출발점 v 를 방문하는 것으로 시작
-> 다음으로 v 에 인접하고 아직 방문하지 않은 정점 w를 선택하여 w를 출발점으로 다시 깊이 우선 탐색을 시작함
-> 두 과정을 모든 정점을 한 번씩 방문 할 때까지 반복함
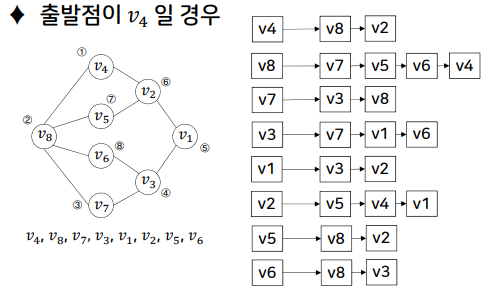
깊이 우선 탐색
- 만약 인접한 모든 정점들이 이미 방문한 정점인 경우는 가장 최근에 방문했던 정점 중에서, 방문하지 않은 정점 w 를 가진 정점을 선택하여 정점 w 로부터 다시 깊이 우선 탐색을 시작함
- 미 방문 정점이 없으면 탐색을 종료함
깊이 우선 탐색 무방향 그래프

순환 호출을 이용한 깊이 우선 탐색
void DFS(int v){
int w;
extern int VISITED[];
VISITED[v] = 1;
while(v에 인접한 모든 정점 w)
if(!VISITED[w])
DFS(w); }
스택을 직접 운영하는 깊이 우선 탐색
void DFS(int v){
int n,w ;
extern struct stack*s;
extern int VISITED[];
InitializeStack(s);
push(s,v);
VISITED[v]=1;
while((n=pop(s))>=0){
VISITED[n]=1;
while(n에 인접한 모든 정점 w){
if(!VISITED[w]){
push(s,w); } } } }
너비 우선 탐색
- 출발점 v를 방문하는 것으로 시작함
-> 다음으로 v에 인접한 정점 w를 모두 방문한 후 다시 w에 인접한 방문하지 않은 정점들을 차례로 방문함
-> 두 과정을 모든 정점을 한 번씩 방문할 때까지 반복함
- 너비 우선 탐색은 인접 정점을 모두 방문하기 때문에 스택이 필요하지 않고, 대신 큐를 사용함


큐를 이용한 너비 우선 탐색
void BFS(intv){
int w;
extern struct queue*q;
VISITED[v]=1;
InitializeQueue(q);
AddQueue(q,v);
while(!q_empty()){
v = DeleteQueue(q);
while(v에 인접한 모든 정점 w){
if(!VISITED[w]){
AddQueue(q,w);
VISITED[w]=1; } } } }
'방송통신대학 > 자료구조' 카테고리의 다른 글
| 15-2. 최소신장트리 (0) | 2021.01.16 |
|---|---|
| 14-2. 그래프 표현법, 추상자료형 (0) | 2021.01.14 |
| 14-2. 그래프 표현법, 추상자료형 (0) | 2021.01.14 |
| 14-1. 그래프 (0) | 2021.01.13 |
| 13-3. 레드 블랙 트리 (0) | 2021.01.12 |