02. Splay 트리
이진 탐색 트리의 단점
- BS트리의 성능은 트리의 구조와 특정 노드에 접근할 확률에 영향을 받음
- 트리의 성능이 구조에 영향을 받기 때문에 어떤 노드의 탐색/삽입/삭제를 위한 접근 정보를 예측할 수 없는 상황에서는 최적의 BS트리구조를 결정하기 어려움
- 휴리스틱 알고리즘을 사용하여 구축한 BS트리의 성능이 최적에 가까움
이진 탐색 트리의 성능
: 좋은 성능의 BS트리를 구축하는 방법 (휴리스틱)
→ 자주 탐색하는 키를 가진 노드를 트리의 루트에 가깝게 놓는다.
→ 트리가 균형(balance)이 되도록 유지한다. 즉,각 노드에 대해 왼쪽과 오른쪽 서브 트리가 가능한 한 같은 수의 노드를 갖게 한다.
Splay트리
- 자주 탐색하는 키를 가진 노드를 루트에 가깝게 위치하도록 구성한 BS트리
- Splay연산 : 최근에 접근한 노드 x를 (곧 사용할 것으로 예상하여)루트에 위치시켜 트리를 재구성하는 연산
- Splay트리 : 가장 최근에 사용한 노드 x가 트리의 루트에 올 때까지 Splay연산을 반복하여 적용하여 생성된 이진트리
Splay트리의 연산

노드 x : 최근에 접근한 노드,
노드 p : x의 부모 노드,
노드 g: x의 조부모(부모의 부모) 노드
① Zig : p가 트리의 루트면 p와 x의 간선 연결(edge joining)을 회전시킨다.
② Zig-Zig : p가 루트가 아니고 x와 p가 동일하게 왼쪽 자식들 또는 오른쪽 자식들이면 p와 조부모 g와의 간선 연결을 회전시키고 그다음에 x와 p의 간선 연결을 회전시킨다.
③ Zig-Zag : 만약 p가 루트가 아니고 x가 왼쪽 자식, p가 오른쪽 자식(또는 그 반대)이면 x와 p의 간선 연결을 회전시키고 그 다음에 x와 x의 새로운 부모 p와의 간선 연결을 회전시킨다.
Splay트리의 연산 (Zig회전(단일 회전))
Zig : p가 트리의 루트 노드이면 p와 x의 간선 연결(edgejoining)을 회전시킨다.

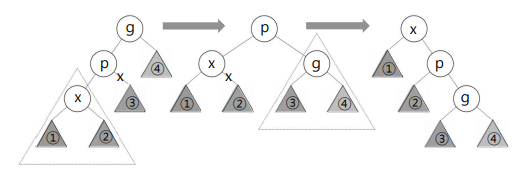
Splay트리의 연산(Zig-Zig회전(두 개의 단일 회전))
Zig-Zig : p가 루트가 아니고 x와 p가 동일하게 왼쪽 자식들 또는 오른쪽 자식들이면 p와 조부모 g와의 간선 연결을 회전시키고 그 다음에 x와 p의 간선 연결을 회전시킨다.
Splay트리의 연산의 적용
- 왼쪽 트리에 대해 7이 루트가 되도록 Splay연산을 적용

'방송통신대학 > 자료구조' 카테고리의 다른 글
| 12-1. 멀티웨이 탐색 트리 (0) | 2021.01.07 |
|---|---|
| 11-3. AVL트리, BB트리 (0) | 2021.01.06 |
| 11-1. 이진 탐색 트리(binary search tree) 응용 (0) | 2021.01.04 |
| 10-3. 이진트리 개수 (0) | 2021.01.03 |
| 10-2. 숲 (0) | 2021.01.02 |